Урок-конференция для учащихся 11 класса, посвященный Н.И. Лобачевскому

^{Муниципальное образовательное учреждение «Школа-лицей №1», г. Алушты}

^{Автор разработки}

^{учитель математики}

^{Блезарова Сусанна Велиевна}

^Цель^{: ознакомить учащихся с корифеем математической науки, с геометрией Лобачевского.}

^{Оборудование}^{: портреты Н. И. Лобачевского и Евклида, газеты посвященные биографии Н. И. Лобачевскому и Евклида, презентация, выставка научной литературы о биографии известных математиков, чертежи, модели.}

^{Ход урока}^:
^{1. Краткая биография Н. И. Лобачевского.}
^{2. Из воспоминаний современников о Н. И. Лобачевском.}
^{3. Беседа о геометрии Лобачевского.}
^{4. Презентация.}
^{5. Викторина.}
^{6. Заключительная часть.}

^{Всю подготовительную работу проводили учащиеся: подготовили выступление, газету, презентацию, викторину, чертежи, модели. С беседой о геометрии выступил учитель.}

^{Ученики открывают конференцию:}

^{1 ученик}^{: Высокий лоб, нахмуренные брови.}

^{В холодной бронзе — отражённый луч…}

^{2 ученик}^{: Но даже неподвижный и суровый, он, как живой,}

^{Спокоен и могуч.}

^{3 ученик}^{: Когда-то здесь, на площади широкой,}

^{На этот вот Казанской мостовой,}

^{Задумчивый, неторопливый, строгий}

^{Он шёл на лекции- великий и живой.}

^{1 ученик}^{: Пусть новых линий не начертят руки-}

^{Он здесь стоит, взнесённый высоко,}

^{2 ученик}^{: Как утверждение бессмертья своего.}

^{3 ученик}^{: Как вечный символ торжества науки.}

^{Слово предоставляется учащимся (3−4 докладчика), которые подготовили доклады о биографии Н. И. Лобачевского.}

^{Докладчики:}

^{Николай Иванович Лобачевский (1792−1856) — великий математик, профессор и ректор Казанского университета. Н. И. Лобаческий воспитывался и учился в Казанской гимназии, а затем в Казанском университете. Своими замечательными успехами рано обратил на себя внимание профессоров. По характеристике университетской инспекции Лобачевский был юноша упрямый, нераскаянный, проявляющий даже «признаки безбожия».}

^{Только поддержка и заступничество профессоров помещали исключению Лобачевского из университета. Блестящая аттестация со стороны профессоров о математических дарованиях Лобачевского и их настойчивое ходатайство перед начальством были причиной оставления Лобачевского для научной и педагогической деятельности в университете.}

^{В 19 лет Лобачевский получил степень магистра, а в 24года был экстраординарным, а потом ординарным профессором Казанского университета. В 1827 году был избран ректором Казанского университета и в этой должности находился непрерывно 19 лет (переизбирался 6 раз подряд). Деятельность Лобачевского вызывает изумление. Наряду с большой административной и педагогической работой, он много занимался наукой. Лобачевский прославил себя и российскую науку открытой им новой геометрии, носящей его имя. Геометрия Лобачевского явилась подлинной революцией в науке и положила начало новой геометрии, называемой неевклидовой. Это открытие оказало благотворное влияние на дальнейшее развитие математики как науки и некоторых разделов физики.}

^{Свои идеи Лобачевский изложил в сочинениях: «О началах геометрии», «Воображаемая геометрия», «Новые начала геометрии с полной теорией параллельных линий», «Пангеометрия».}

^{Без кипучей и страстной деятельности на пользу своего народа Лобачевский не мыслил своего существования. Несмотря на душную атмосферу николаевской реакции, не имея, ни моральной, нм материальной поддержки со стороны официальных кругов, Лобачевский стойко выдержал борьбу за признание своих идей, которые по-настоящему были оценены только после его смерти.}

^{Беседа учителя о геометрии Лобачевского.}

^{Учитель:}

^{В течение двух тысяч лет учёные всех стран считали, что иной геометрии, кроме евклидовой, быть не может. Однако пятый постулат Евклида (аксиома о параллельности прямых: через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой), вызвал у многих учёных попытки дать его доказательство на основании остальных аксиом Евклида. Н. И. Лобачевский в феврале в 1826 г. показал недоказуемость аксиомы параллельных линий тем, что построил неевклидовую геометрию, названную геометрией Лобачевского, в основе которой лежат все аксиомы евклидовой геометрии, за исключением пятого постулата, который он заменил своим: «Через точку взятую вне прямой на плоскости, можно провести бесчисленное множество прямых не пересекающих данную.»}

^{Исходя из указанных выше аксиом, принятых геометрией Лобачевского, доказываются следующие предположения:}

^{1. Пепендикуляр и наклонная к одной и той же прямой, расположенные в одной плоскости, могут и не пересекаться.}

^{2. Сумма всех внутренних углов треугольника меняется от треугольника к треугольнику, но всегда меньше 2d.}

^{3. Сумма всех внутренних углов всякого выпуклого чётырехугольника меньше чем 4d.}

^{Отсюда как следствие вытекает: не существует прямоугольников.}

^{4. Подобных фигур с коэффициентом подобия, отличным от единицы, не существует. В частности, для данного треугольника нельзя построить подобный, но не равный ему треугольник.}

^{5. Не вокруг всякого треугольника можно описать окружность.}

^{6. Геометрическое место точек, равноудалённых от данной прямой в расположенных по одну сторону от неё на плоскости, не может быть прямой (есть всегда кривая линия)}

^{Реальна ли геометрия Лобачевского?}

^{Это геометрическое предположение, принимаемое нами без доказательства, как исходное, позволяющее вскрыть геометрическое содержание точек, прямых и плоскостей в их взаимном расположении. (Учитель знакомит учащихся с примером необыкновенного истолкования евклидовой геометрии, когда за «точку» принимается шар радиуса r, за «прямую» — бесконечный круговой цилиндр радиуса r, за «плоскость» — плоскопараллельная пластинка толщиной 2r.)}

^{В школьном курсе геометрии представление о прямой даёт туго натянутая нить, представление о плоскости — поверхность хорошо отполированного гладкого зеркала (это одно из возможных, более простых и привычных истолкований). Нарисуем на листке бумаги треугольник. Сторонами его являются прямые в обычном их истолковании. Если свернём этот лист в форму цилиндра, то стороны треугольника на поверхности цилиндра будут, вообще говоря, кривыми. Эти кривые при развёртывании цилиндра на плоскость, конечно, опять переходят в прямые. Линии на поверхности цилиндра, которые при развёртывании цилиндра на плоскость переходят в прямые, называются}^{геодезическими линиями}^{цилиндра.}
^{Геодезическими линиями какой — нибудь поверхности называют линии кратчайшего расстояния между точками поверхности.}

^{Если за «точки» принять точки цилиндра, а за «прямые» — геодезические линии цилиндра, тогда на цилиндре будет выполняться планиметрия евклидовой геометрии. Действительно, сумма углов геодезического треугольника, как легко догадаться, равняется двум прямым. А это утверждение эквивалентно пятому постулату.}

^{Далее по рисунку сферы или её модели строят объяснение геометрии сферы.}

^{В докладе принимают участие докладчик и его оппоненты (2−3 уч.)}

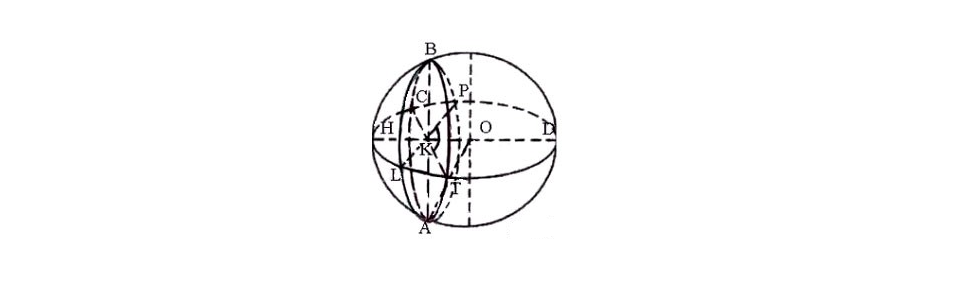
^{Докладчик:}^{Посмотрим, какая геометрия выполнятся на сфере, если за «точки» принять точки этой сферы, а за «прямые" — её геодезические линии. (Нужно заметить, что сфера путём изгибания на плоскость не развёртывается, и геодезические линии её не могут, как у цилиндра, переходить в прямые). Геодезическими линиями на сфере, оказывается, являются дуги больших кругов. Дуги больших кругов, как имеющие общий центр в центре сферы, попарно пересекаются. Поэтому на сфере нет параллельных «прямых». Следовательно, через «точку», взятую вне «прямой», в данном случае нельзя провести ни одной параллельной «прямой». Характерной особенностью этой геометрии сферы является то, что сумма внутренних углов «прямолинейного» (геодезического) треугольника больше двух прямых. Этот факт легко усматривается на чертеже и модели сферы.}

^{Оппонент № 1:}^{Геометрия сферы есть простейшая модель так называемой неевклидовой геометрии Римана. Немецкий математик Риман (1826 -1866) открыл свою геометрию после того, как ознакомился с геометрией Лобачевского.}

^{Оппонент № 2:}^{Геометрия Лобачевского (планиметрия) выполняется на поверхности псевдосферы (демонстрируется модель этой поверхности и в кратких словах, при помощи специально изготовленных чертежах, объясняет её получение как поверхности вращения трактриссы вокруг её оси). Если на этой поверхности начертить геодезический треугольник (геодезические линии на модели получаются при помощи туго натянутой нити, натёртой мелом и зажатой в двух вершинах треугольника), то сумма углов такого треугольника будет уже меньше двух прямых, т. е. будет как раз выполняться то, что утверждает геометрия Лобачевского. Этот факт легко усматривается на модели и на специально изготовленном чертеже.}

^{4. Учащимся предлагается презентация, подготовленная учащимся Пивненко С., в которой проводится сравнение с основными аксиомами двух геометрий: геометрией Евклида и геометрией Лобачевского.(см приложение)}

^{А теперь проведём викторину, посвященную биографии Н. И. Лобачевского.}

^{1. Сколько было лет, когда Н. И. Лобачевский окончили университет?}

^Ответ.^{В 19 лет окончил Казанский университет с присуждением степени магистра наук.}

^{2. Н. И. Лобачевскому в гимназии не понравилось. Он сбежал домой, но через некоторое время приехал обратно. Лобачевский прочитал один рассказ и подумал: «Он бы не бросил учёбу». Он — кто это? Благодаря кому Николай Иванович снова оказался в гимназии?}

^Ответ.^{Михаилу Ломоносову.}

^{В куче старых пожелтевших от времени газет Коля нашёл истрёпанную небольшую книжку. Это был рассказ о том, как сын простого рыбака-помора с далёкого севера зимой отправился учиться в Москву.}

^{«Бывают же такие, — подумал Коля, прочитав эту книжку. — Не побоялся. Ушёл один из родной деревни. В лютую стужу догнал обозы… А я-то? Учиться бросил. Из-за чего? Ломоносов не бросил бы».}

^{3. В 9 лет по Николай Иванович поступил в гимназию. Как прошёл его первый день?}

^Ответ.^{В первый же день учёбы в гимназии Коля Лобачевский был наказан за то, что заступился за одноклассника.}

^{Схватив за воротник, учитель потащил его в угол и заставил стоять на коленях до конца урока с кочергой в руках.}

^{4. Как Лобачевский называл свою геометрию?}

^Ответ.^{«Воображаемая геометрия», «пангеометрия», то есть всеобщая геометрия. Теперь во всём мире называют «геометрией Лобачевского».}

^{5. 1830 год. Лобачевский третий год работает ректором Казанского университета. На Казань и Поволжье обрушилась беда — эпидемия холеры. Энергичными и самоотверженными действиями Николая Ивановича удалось предотвратить проникновение холеры на университетскую территорию. И хотя холера выкосила в городе половину населения, среди студентов и служащих университета, заболевших было совсем немного. Из 660 человек, чьё здоровье он защищал, умерло только 16 человек, меньше 3%.}

^{Как ему это удалось?}

^Ответ^{. Чтобы спасти преподавателей и студентов, Лобачевский поселил их вместе с семьями в университете. Это помогло избежать трагедии, которая постигла город.}

^{6. В каком возрасте он стал профессором?}

^Ответ^{. Профессором стал в 24 года.}

^{15. Какой известный русский писатель учился в Казанском университете, когда Лобачевский работал ректором?}

^Ответ^{. Лев Николаевич Толстой.}

^{Задача, которую Коля Лобачевский решил устно на вступительных испытаниях в гимназию:}

^{Бассейн получает воду из четырех труб; первая наполняет его за 1час, вторая — за 2часа, третья — за 3часа, а четвёртая — за 4часа. Сколько потребуется времени для наполнения бассейна, если все четыре трубы открыть одновременно?}

^{Заключительное слово учителя:}

^{Таким образом, геометрия Лобачевского (планиметрия) нашла своё реальное истолкование на поверхности псевдосферы, т. е. эта геометрия реальна, в такой же мере, как геометрия Евклида, Римана. Которые реальны, поскольку они выполняются на реальных поверхностях.}

^{Открытие Лобачевского составляет целую эпоху в науке. Идеи Лобачевского находят широкое отражение в современной физике (теория относительности).}

^{Итог урока}^{: оцениваются выступления докладчиков, помощь оппонентов.}